Eric Pauley
Pre-takeoff checklist
Note: I am updating this post incorporating feedback from below.
In 2021, the FAA released AD 2020-26-16, requiring inspection of most PA28/32 wing spars. This AD also required reporting results of the inspections to the FAA and Piper. This data has not been made publicly available, until now.
In October, 2022, I submitted a Freedom of Information Act (FOIA) request to the FAA for a complete copy of all inspection results reported to the FAA. I received data back from this request in March of 2024. The raw data, including my analysis, is publicly available at https://github.com/ericpauley/piper_wingspar
Given this data, I had two key research questions:
1. Are ECI failures consistent with fatigue (which is additive and would be consistent with life-limiting components), or with random occurences such as hard landings, which suggest recurrent inspections but are not consistent with life limits.
2. Are Factored Service Hours/Commercial Service Hours an accurate depiction of risk? What is the relative hazard of commercial and non-commercial service hours?
General Trends
Up until this point, the FAA has only released some general data in SAIB 2022-20; this was mostly anecdotal data on high-time wing spars that failed ECI. However, this did not include information on the number of aircraft inspected (there is a bias in the data as low-time planes were not required to perform the AD). Let's look at a histogram of failed spars by time in service:

This may look like more failures in high-time spars, but let's look at the spars that didn't fail too:

Here, outcome "True" is passed and "False" is failed. Basically, the failures roughly follow the spars that were tested. Let's instead look at the failure rate by different aged spars (based on Factored Service Hours):

Here, each bar represents a bucket of ages (first bucket is 0-2500 FSH and so on). The lines represent 95% confidence intervals for the actual failure rate. In effect, differences in failure rates past 5000 hours are not statistically significant. Of course, we would expect spars with more time to be more likely to fail, simply because they have had more time to be damaged. The real question is whether what we are seeing is fatigue (i.e., stress that accumulates and will eventually cause failure) or accumulated possibilities for random damage, such as from a hard landing.
Determining Failure Distribution
If spar ECI failure is a result of occurences such as hard landings, we would expect these failures to be memoryless: effectively, every flight hour is a roll of the dice, and a spar accumulates more chances for damage over time. This would mean several things:
* A spar can experience ECI failure at any time, even with low hours
* A spar is just as likely to go from good to bad in hours 0-5000 as in hours 10000-15000
In statistics, this is known as a Poisson process, and is characterized by the Mean Time Between Failures (MTBF). Let's proceed under the assumption that spar failure is a Poisson process. We can use Maximum Likelihood Estimation to determine a candidate MTBF that makes the observed outcome most likely. I did this analysis computationally and found the MTBF of piper wing spars to be roughly 375,000 Factored Service Hours. This gets us part way there, but still follows the FAA's assumption that one commercial hour is equivalent to 17 non-commercial hours.
Next, we'll try to determine the hazard ratio between commercial and non-commercial hours. We'll do the same MLE as above, but this time determine the hazard ratio as well.
Result: The MTBF of piper wing spars is 510,000 hours, with commercial hours counting for 1.17 non-commercial hours.
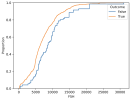
To visualize this, let's look at the cumulative distribution of overall spars, failed spars, along with the spar failures we'd expect to see under this model:

The failure distribution (in orange) almost exactly matches the expected failure distribution (in green) under purely random failure rates. We can use a goodness-of-fit test to determine whether this matches the ECI failures reported to the FAA. This test yields a p-value of 0.88, which strongly implies (though does not prove!) that ECI failures are consistent with this memoryless process and not with fatigue.
TL;DR: My conclusions from analysis of 8500 Piper wing spars suggest:
1. Failures are memoryless (i.e., not necessarily caused by fatigue) with an average MTBF of 510,000 non-commercial hours, and with commercial hours counting for 1.17 non-commercial hours.
2. There is insufficient data from the AD to say anything about the increased failure rate of ultra-high-time spars
3. Spars can fail ECI at any time, even with low TIS, FSH, or CSH. This is inconsistent with the initial inspection delay of 4500-5000h in SB1372.
4. The evidence from the spar AD inspection reports does not support a life limit on wing spars (note: other sources like accelerated lifecycle testing could indicate otherwise. I'm a computer scientist and statistician, not a structural engineer!)
5. The results do suggest recurrent inspections, but not the 4500-5000h initial wait that Piper currently recommends in SB1372. The period between these inspections depends on a variety of factors, including the MTBF that I've determined above.
In 2021, the FAA released AD 2020-26-16, requiring inspection of most PA28/32 wing spars. This AD also required reporting results of the inspections to the FAA and Piper. This data has not been made publicly available, until now.
In October, 2022, I submitted a Freedom of Information Act (FOIA) request to the FAA for a complete copy of all inspection results reported to the FAA. I received data back from this request in March of 2024. The raw data, including my analysis, is publicly available at https://github.com/ericpauley/piper_wingspar
Given this data, I had two key research questions:
1. Are ECI failures consistent with fatigue (which is additive and would be consistent with life-limiting components), or with random occurences such as hard landings, which suggest recurrent inspections but are not consistent with life limits.
2. Are Factored Service Hours/Commercial Service Hours an accurate depiction of risk? What is the relative hazard of commercial and non-commercial service hours?
General Trends
Up until this point, the FAA has only released some general data in SAIB 2022-20; this was mostly anecdotal data on high-time wing spars that failed ECI. However, this did not include information on the number of aircraft inspected (there is a bias in the data as low-time planes were not required to perform the AD). Let's look at a histogram of failed spars by time in service:

This may look like more failures in high-time spars, but let's look at the spars that didn't fail too:

Here, outcome "True" is passed and "False" is failed. Basically, the failures roughly follow the spars that were tested. Let's instead look at the failure rate by different aged spars (based on Factored Service Hours):

Here, each bar represents a bucket of ages (first bucket is 0-2500 FSH and so on). The lines represent 95% confidence intervals for the actual failure rate. In effect, differences in failure rates past 5000 hours are not statistically significant. Of course, we would expect spars with more time to be more likely to fail, simply because they have had more time to be damaged. The real question is whether what we are seeing is fatigue (i.e., stress that accumulates and will eventually cause failure) or accumulated possibilities for random damage, such as from a hard landing.
Determining Failure Distribution
If spar ECI failure is a result of occurences such as hard landings, we would expect these failures to be memoryless: effectively, every flight hour is a roll of the dice, and a spar accumulates more chances for damage over time. This would mean several things:
* A spar can experience ECI failure at any time, even with low hours
* A spar is just as likely to go from good to bad in hours 0-5000 as in hours 10000-15000
In statistics, this is known as a Poisson process, and is characterized by the Mean Time Between Failures (MTBF). Let's proceed under the assumption that spar failure is a Poisson process. We can use Maximum Likelihood Estimation to determine a candidate MTBF that makes the observed outcome most likely. I did this analysis computationally and found the MTBF of piper wing spars to be roughly 375,000 Factored Service Hours. This gets us part way there, but still follows the FAA's assumption that one commercial hour is equivalent to 17 non-commercial hours.
Next, we'll try to determine the hazard ratio between commercial and non-commercial hours. We'll do the same MLE as above, but this time determine the hazard ratio as well.
Result: The MTBF of piper wing spars is 510,000 hours, with commercial hours counting for 1.17 non-commercial hours.
To visualize this, let's look at the cumulative distribution of overall spars, failed spars, along with the spar failures we'd expect to see under this model:

The failure distribution (in orange) almost exactly matches the expected failure distribution (in green) under purely random failure rates. We can use a goodness-of-fit test to determine whether this matches the ECI failures reported to the FAA. This test yields a p-value of 0.88, which strongly implies (though does not prove!) that ECI failures are consistent with this memoryless process and not with fatigue.
TL;DR: My conclusions from analysis of 8500 Piper wing spars suggest:
1. Failures are memoryless (i.e., not necessarily caused by fatigue) with an average MTBF of 510,000 non-commercial hours, and with commercial hours counting for 1.17 non-commercial hours.
2. There is insufficient data from the AD to say anything about the increased failure rate of ultra-high-time spars
3. Spars can fail ECI at any time, even with low TIS, FSH, or CSH. This is inconsistent with the initial inspection delay of 4500-5000h in SB1372.
4. The evidence from the spar AD inspection reports does not support a life limit on wing spars (note: other sources like accelerated lifecycle testing could indicate otherwise. I'm a computer scientist and statistician, not a structural engineer!)
5. The results do suggest recurrent inspections, but not the 4500-5000h initial wait that Piper currently recommends in SB1372. The period between these inspections depends on a variety of factors, including the MTBF that I've determined above.
Attachments
Last edited: