Matthew
Touchdown! Greaser!
Started puzzling over this today. I won't be able to get back to it until sometime next week, though.
Given: A turntable, a center pivot point, and an extension shaft off to one side. At the end of the shaft is a link that is a fixed length. As the shaft extends or retracts, the link that's attached to the end of the shaft will push or pull on the turntable and rotate it within physical limits.
I don't have a good drawing package handy, so this is as good as it gets.
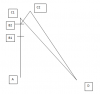
A-B1 represents the extension shaft at a "zero" position. A-B2 represents the shaft as it is extended. B1- C1 represents the link at the "zero" position, and B2-C2 presents the link at the the extended position where Bx and Cx are the attach points. D is the pivot point of of the turntable. And D-C1, as well as D-C2, is the radius.
The shaft can also retract, but I didn't show that part. When the shaft retracts, the link will pivot in the opposite direction.
I know the distance A-D. I know the radius (D-C1 and D-C2). I know the length of the link.
The angle between A-D and C1-D should be acos( A-D / C1-D). And since I already know 2 sides of the right triangle I can figure the third, subtract out the fixed length of the link, and come up with the shaft length at this particular position called "zero".
As the shaft extends, it pushes one end of the link, the link pushes where it is attached to the turntable, and the turntable rotates. The points C1 and C2 will be following the arc that is defined by the radius that pivots at point D. The B1 and B2 points will always follow the end of the shaft that can only move along a fixed line. The link is a fixed length, but its angles will change.
What I am trying to calculate:
I need to come up with a way to figure how many degrees of rotation I get as the length of the shaft increases (or decreases). For example: I need to add 5 degrees to that angle, how far does the shaft need to extend? Or, I need to subtract 5 degrees from that angle, how far does the shaft need to retract? (Angle = the angle between A-D-Cx)
I have some ideas on how to approach this, but right now they are in my head and I haven't been able to get them organized enough to put them on paper. And, as I said, it's going to be sometime next week before I can get back to it.
Any thoughts?
Given: A turntable, a center pivot point, and an extension shaft off to one side. At the end of the shaft is a link that is a fixed length. As the shaft extends or retracts, the link that's attached to the end of the shaft will push or pull on the turntable and rotate it within physical limits.
I don't have a good drawing package handy, so this is as good as it gets.

A-B1 represents the extension shaft at a "zero" position. A-B2 represents the shaft as it is extended. B1- C1 represents the link at the "zero" position, and B2-C2 presents the link at the the extended position where Bx and Cx are the attach points. D is the pivot point of of the turntable. And D-C1, as well as D-C2, is the radius.
The shaft can also retract, but I didn't show that part. When the shaft retracts, the link will pivot in the opposite direction.
I know the distance A-D. I know the radius (D-C1 and D-C2). I know the length of the link.
The angle between A-D and C1-D should be acos( A-D / C1-D). And since I already know 2 sides of the right triangle I can figure the third, subtract out the fixed length of the link, and come up with the shaft length at this particular position called "zero".
As the shaft extends, it pushes one end of the link, the link pushes where it is attached to the turntable, and the turntable rotates. The points C1 and C2 will be following the arc that is defined by the radius that pivots at point D. The B1 and B2 points will always follow the end of the shaft that can only move along a fixed line. The link is a fixed length, but its angles will change.
What I am trying to calculate:
I need to come up with a way to figure how many degrees of rotation I get as the length of the shaft increases (or decreases). For example: I need to add 5 degrees to that angle, how far does the shaft need to extend? Or, I need to subtract 5 degrees from that angle, how far does the shaft need to retract? (Angle = the angle between A-D-Cx)
I have some ideas on how to approach this, but right now they are in my head and I haven't been able to get them organized enough to put them on paper. And, as I said, it's going to be sometime next week before I can get back to it.
Any thoughts?




